How Big is That Number? Episode 1

This will be the first installment of a new feature I call "How Big is That Number?" in which I try to explain exactly how big that number is.

Dear Dr. Math,
How much space would a googol grains of sand take up?
xoxo,
Frequent Googol Searcher

Dear FreGooSear,

Let me begin by thanking you for reminding us all of the correct spelling of "googol". A lot of people forget that before it inspired the name of an obscure website, the word "googol", as coined by a man named Milton Sirotta back in 1938, referred to the number . I don't know the whole story here, but I'm guessing that as an infant, he somehow wrote a 1 followed by 100 zeroes (I'm guessing in blue crayon), and when asked by his parents what that was, all he could make were baby sounds. Hence the name. Any other explanation seems highly improbable.

So, how big is this number with the silly name? Well, first off, if we wanted to address it in the nomenclature of billions and trillions, it would be known as ten thousand trillion trillion trillion trillion trillion trillion trillion trillion. That's a ten-thousand followed by 8 trillions. Or, if you prefer to think of it in terms of current financial events, $1 googol would be about 12,706 trillion trillion trillion trillion trillion trillion trillion economic stimulus packages.

Now, to answer your question about grains of sand: let's approximate a grain of sand as a cube 1 millimeter across. That would mean that 1000 grains of sand in a row would be 1 meter long. So, one cubic meter would contain 1000*1000*1000, or , grains. A googol grains, therefore, would take up cubic meters of space. And it would really be "space", because this is way bigger than our tiny little planet could accommodate. For comparison, a sphere the size of the Earth (which has a radius of about 6,371 kilometers, or 6,371,000 meters) has, according to the formula for the volume of a sphere, a volume equal to cubic meters, about grains of sand, so it would take about Earth-sized balls of sand to get a googol grains. Alternatively, if you lumped all the sand together into one giant ball, you'd need cubic meters, and solving for R gives us a radius of approximately meters, which is about 140 trillion light years, or 10,000 times bigger than the size of the observable universe. So maybe space itself wouldn't even be big enough to handle such a massive sand ball.

Carrying the sand idea a little further, imagine there was a huge interstellar alien for whom the Earth appeared to be as small as a grain of sand is to us. Now, suppose this being lived on a giant planet, the planet Gigantica, as big, relative to the alien, as the Earth is to us. This would imply that the volume of Gigantica was in proportion to the Earth as the Earth is to a grain of sand, about times as big; so Gigantica itself would be about cubic meters in volume. If, in turn, there were a still larger alien for whom Gigantica looked like a grain of sand and who lived on an even larger planet, the planet Humonga, say, then Humonga would have to be times as big as Gigantica, for a volume of cubic meters. Now, if yet an even larger alien, from the planet Ginormica, looked down on Humonga as a tiny grain of sand, it would require Humonga-balls to comprise a volume of cubic meters, which you'll recall was the volume of space taken up by a googol grains of our puny Earth-sand. Back here on Earth, grains of sand is 10 cubic meters, about the volume of a nice 10 meter by 10 meter patch of beach (assuming a depth of 10 centimeters). So on Ginormica, this giant giant giant alien could kick back in a beach chair, sip a giant giant giant beer and build a giant giant giant sand castle out of those googol grains with plenty of sand left over to get in its megashoes.

-DrM

Unexpected Values, part 3

And now, the exciting conclusion!


Dear Dr. Math,
My college administration says that the student-teacher ratio is 5:1. But all my classes have like 30 people in them. What gives? Are they just lying?
Sincerely,
A Student at a Local College

Well, ASAALC, that depends on what you mean by "lying." If you mean, Are they miscalculating their student-faculty ratio?, then the answer's probably "no." These things are public information, and anyone with a calculator can divide the number of students by the number of teachers. (Whether they include non-teaching faculty, like that weird guy who lives in the basement and hasn't taught a class since the 60s, is kind of an ethical gray-area.) However, if the question is, Are they misleading people by reporting a somewhat meaningless statistic?, then "yes." Here's how the magic trick works:

It all comes back to the idea of average, and the different things the word "average" means to people. Many people think of "average" as meaning "typical" or "to be expected," a misperception that isn't helped any by the synonym "expected value." So, if a college reports that it has a student-teacher ratio of 5:1, or equivalently, that it has an average class size of 5, people leap to the conclusion that the typical class they'll encounter at the college will have 5 people in it (and how awesome is that?!). However, that may not be the typical experience, and it may even be impossible. Let's take a look at a simple example:

If I told you that my girlfriend and I were going to flip a coin and decide whether to have a baby based on the result,* the average number of babies we would have, i.e., our expected number of babies, would be 1/2. But of course, we would be surprised, even shocked, if we actually had half a baby. In this case, the "expected" value is anything but. The value 1/2 just represents the plausibility we associate to the chance of having one baby. If we repeated the experiment many times, the ratio of babies to attempts would converge to 1/2.

Similarly, suppose that a tiny school had 10 total students and 2 teachers. So, the student-teacher ratio is 5:1. Now, let's say one of the teachers is that awesome guy who lets you call him by his first name, and the other has really bad dandruff or something, so 9 people register for Class #1 and only 1 person registers for Class #2. The average class size is the average of 9 and 1, which is 5--equal to the ratio of students to teachers, as it should be. However, if I picked a random student and asked him (it's an all boys' school) how many people were in his class, 9 times out of 10 he would say 9, and 1 time out of 10 he would say 1. So the average response I would get would be , for a difference of 3.2! In fact, the only way the two numbers can actually be the same is if all the classes are exactly the same size.

If you think about it, it makes perfect sense that I'd get someone in a larger class more often in a random poll, since the larger classes have more people in them to get polled. The question, then, is which of these numbers actually represents the "typical" student experience. Since the student-teacher ratio is generally smaller, the schools are happy to just report that and hope you don't notice the difference. What they really should be reporting is something more like the distribution of class sizes. As it is now, if you want to know what the classes are like, you've just got to go see for yourself.

Also, what's the deal with the vending machine only having Pepsi?

-DrM

*For the record, that's not how we do it. We roll a 20-sided die.

Unexpected Values, part 2

Dear Dr. Math,
Is it ever a good idea to play the lottery? My dad says he only buys a ticket when the jackpot is bigger than the odds against winning, but we're still broke.
Angelica

Dear Angelica,

NO!!

-DrM

P.S.--Here's why:

Hopefully, by now you've read my previous post all about expected values. (If not, go read it now; I'll wait here. OK? OK.) Now, the thing your dad is referring to is the fact, which is a fact, that the expected value of the lottery is occasionally greater than $1, the cost of the ticket. Assuming you play the Powerball, which is the most popular lottery in the U.S., your odds of winning the jackpot are 1 in 195,249,054. (If you'd like, I'll show you how to compute that sometime.) So, considering only the jackpot, if the payoff is higher than $195,249,054, the expected value of the lottery, i.e., the jackpot times the probability of winning, would actually be greater than the cost, so it would seem that math is telling us to play. However, this is still not a convincing argument, even putting aside other practical concerns involved in winning the lottery.*

The reason comes back to the idea of variance, which I also talked about last time. Just so you can follow along at home, the variance of a simple game like this is computed like so: you take the payoff squared times the probability of winning and subtract the expected value squared. So let's say, for example, that the jackpot was $200 million one week. Then the expected value would be the probability of winning times the jackpot, which is , about $1.02. The variance, therefore, is . Mamma mia! That's a lot of variance!

If you remember from last time, the problem with having too high a variance in a bet is that you typically run out of money before you get to win--the distribution of your winnings/losses is too spread out. So, in effect, if you had unlimited funds (which I know for a fact you don't, Angelica) and you could play the lottery with the same odds every week for several billion years, it might actually be a good investment, because on average you would win back $1.02 for every $1 you gambled, a nice healthy 2% return. However, since you're only going to play it at most a few hundred more times (and hopefully no more after today!), the variance is just too high for you to handle. It's kind of a paradox, really, that the decision to place a particular bet once depends on your ability/plans to bet many times. What we see here is an interesting example of the tradeoff between expected value and variance. Sometimes, depending on your circumstances, it's worth sacrificing a little of one to improve the other. If someone offered you $0.99 for your $1 lottery ticket, for example, I'd recommend you sell, no matter how high the jackpot is.

Incidentally, in my opinion, this is how the banking industries and insurance industries make money (or, at least, used to back when they existed). Let's say you're deciding whether to insure your $100,000 house at a cost to you of $1,500. For argument's sake, let's say you have an extra $100,000 in savings that you could use to replace the house if need be, so the only cost is monetary. And let's assume that the chance of your house being completely destroyed is ; you know it, and the insurance company knows it. So, you're trading a bet (no insurance) with an expected loss of but a fairly high variance for a sure-thing loss of $1,500 (if your house burns down, you don't lose anything except the time it takes to file an insurance claim and replace your stuff) and no variance at all. But the extra peace of mind is worth something to you, so maybe you're willing to pay the $500 premium for it. Meanwhile, the insurance company (and the bank that underwrites your policy) is buying millions of these bets, and so their distribution of income is turning into a bell curve, narrowing down pretty much to a fine point centered around a $500 profit per policy. Voilà, everyone wins, but they win more simply by virtue of already being large. (The problem occurs when they start taking that money and doubling down on risky investments, unless they get bail... oh wait, never mind.)

-DrM

*The diminishing marginal utility of money, the chance of having to split winnings with another person, the amount lost to income tax, and the failure to adjust for inflation, to name a few.

Unexpected Values, part 1

I've gotten a lot of questions all related to the idea of averages, so I'm going to devote the next 3 posts to discussing different facets of averaging. It'll be like a trilogy, but hopefully one more like Lord of the Rings than Jurassic Park. Stay tuned to find out!


Dear Dr. Math,
Is there a difference in roulette between betting on black versus betting on a number, like 6? What about betting both at the same time? I usually have more fun betting on black, because my guess is that by betting on black I lose money more slowly, but I'm not sure which is actually better.
Sean

Dear Sean,

My first rule of gambling is don't gamble. (The second rule of gamb.... OK, you get the idea.) But I wouldn't be much of an advice columnist if I told you to do something just because I said so, without helping you understand why. So, maybe after we dissect this gambling question we can talk about why gambling is generally a bad idea. Then we'll talk about why you should sit up straight and why you didn't call me on my birthday.

OK, first: why the bets are the fundamentally the same, and second: why they're different.

The most rudimentary way of analyzing the quality of a bet is computing what's called its expected value. This is the number you get by multiplying each possible payoff by its probability and adding them all together. In roulette, and most other casino games, both the payoffs and the probabilities are well-known, so the expected value is easy to compute. As a convention, we always compute the expected value for a bet of $1 (my kind of bet), but for you high-rollers who bet $n, you can just multiply the end result by n. In the first example, your bet on black, there are 18 ways to win (the 18 black pockets) and 20 ways to lose (the 18 red pockets and the 2 green ones), and we're assuming that every pocket is equally likely, so the probability of winning is . 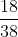If you win, you get $2--your original $1 back plus another one from the house. 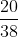If you lose, which happens with probability , you get nothing but my condolences, which have no cash value. 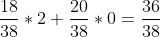So altogether your expected value is , or $0.946. 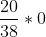Note that the wasn't really doing anything in that calculation, so for simplicity we can skip that part from now on.

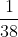
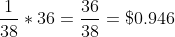
Now, the bet on 6 has a lower probability of winning but a higher payoff, and as we'll see, the two effects cancel each other out exactly. The payoff for winning a bet on 6 is $36, including your $1 plus $35 of the house's, and the probability of winning is , since there's only the one 6 on the wheel, as in life. Hence, the expected value of the bet is again. Those clever French guys in the 18th century managed to design the game of roulette so that almost every bet has that same expected value of $0.946, or 94.6¢. 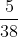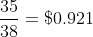Interestingly enough, in America, there is actually one bet which is worse--the "5 number" bet on 0, 00, 1, 2, and 3, which has a payoff of $7 and a probability of , for an expected value of --but since they don't use a 00 in other places, we Americans have that unique opportunity of actually making a worse decision when playing roulette than just playing roulette in the first place.

The reason the expected value matters so much has to do with something I'm sure I'll be talking a lot about in future entries, The Law of Large Numbers, sometimes mistakenly called the "Law of Averages." Essentially (and pay attention to the words I emphasize for clues about how people misuse it), the LLN says that if you keep making the same bet over and over again, in the long run, the total payoff divided by the total number of bets will converge to the expected value of the bet. So, both your bet on black and your bet on 6 will pay you off $0.946 per bet on average, assuming you have enough chips to hang around and keep betting. Notice that this is a bad thing for you and a good thing for the house, because the expected value is less than the price to play the game, $1. I remember being surprised when I went to Las Vegas that so many casinos advertise things like "99% payoffs guaranteed," meaning they're guaranteeing that you lose money?

Also, it's worth mentioning that you can't improve the situation by sneakily combining multiple bets or betting different amounts or any of the other so-called "systems". Expected value has the property that you can compute the expected values of each part of an overlapping bet, like 6 and black, separately and then just add them together. In the end, a bet of $1 bet gives you back an average of $0.946 until you simply run out of money and go home.

The difference, then, between the two kinds of bets has to do with something called their variance, or its square root which goes by the name standard deviation. I'll spare you the formulas (for now), but essentially variance is a measurement of how "spread out" the payoffs of a bet are. So, among all the bets with the same expected value, the bet with the lowest possible variance, which is 0, is the bet where you just hand over your money. The variance gets higher as the payoff gets higher (and the probability of winning gets lower, in order to keep the expected value the same). In the examples above, the bet on black has a variance of about 1.0 and the bet on 6 has a variance of about 33.2, which is substantially larger.

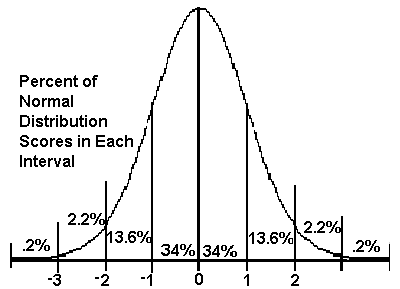
What's going on kind of behind-the-curtain is that over time, if you keep placing the same bet over and over, the distribution of your accumulated winnings takes the shape of a bell curve (by the Central Limit Theorem). The mean of that curve is determined by the expected value of each bet (on account of the LLN); how spread out it is depends on the variance. And if you don't want a lot of risk (of losing or winning), you should try to reduce that spread as much as possible. The casino, for example, would prefer that you just hand over the 5.26 cents you were going to lose on average and repeat. Since that wouldn't be much fun for you, they offer a little variance to keep you entertained. But as you rightly point out, too much variance isn't fun either, because you don't get to "win" very often, and so you might not come back to play again. So it's a delicate balance. Personally, I like the strategy of betting the table minimum on black and red simultaneously and drinking as many free cocktails as possible while my chip stack gradually diminishes. But these are personal decisions.

Bottom line: you can't beat the house, all you can do is maybe make it take a little longer for them to beat you.

-DrM

"in a hole in the grou31;aadn,m vnatoh424..."

Dear Dr. Math,
Suppose you have a computer randomly generating all the characters making up the text of The Hobbit. Suppose the computer generates 200 characters per second. Is there a time period after which it becomes probable that the computer has produced the text of The Hobbit? My gut tells me, "No, it would never happen."
Consider this. If a sufficiently powerful being wanted to write a 20,000 page history of tea-drinking, it could either
(a) produce the book
(b) produce all possible 20,000 page long sequences of keyboard characters
TolkienFan

Dear TolkienFan,

Your question is related to the famous Infinite Monkey Theorem, about a room full of monkeys randomly banging on typewriters for all eternity eventually producing the complete works of Shakespeare. (Digression #1: an English major I knew once joked that the monkeys could reproduce the complete works of D.H. Lawrence in a surprisingly short time.) It turns out that the answer is "yes" in some abstract sense, as long as we're careful about what we mean, but the amount of time it would take is far beyond our comprehension--many many orders of magnitude more than the estimated age of the universe. Here's a quick back-of-the-envelope calculation:

1.) Let's only consider the characters on a standard typewriter. Let's say there are 50 possible characters (including numbers and punctuation, but ignoring capitalization, say), although it turns out not to matter very much whether there are 50 keys or 50,000.

2.) Approximate the length of The Hobbit as 360,000 characters--it's a 320 page book, times a standard 250 words per page, times an average 4.5 letters per word in English.

3.) Assume all characters are equally likely to be output by the random generator, be it computer or monkey. (Digression #2: someone actually did this experiment once with real live monkeys and found that the monkeys were extremely overly fond of the letter "s" for some reason. Also, they [the monkeys] really enjoyed urinating on the keyboard.) Assume the characters are probabilistically independent of each other, i.e., knowing what one character is doesn't inform our knowledge of any other one.

4.) Now, break up the output of the generator into chunks of length 360,000. For each chunk, the chance of the first character being equal to the first character of The Hobbit, which is "i", is . By the assumption of independence, the chance of the first two characters being correct, "in", is , or , and so on. So the chance of the whole block of 360,000 characters reproducing the entire book is , which is about , an astronomically small number. Let's call that number p. The probability of failing to produce The Hobbit in each chunk is (1-p).

5.) If we imagine doing this process a second time, the probability that we'd fail both times is , because of the independence property again. In general if we repeat it n times, the probability of failing all n times is . Now, and this is the key, (1-p) is extremely close to 1 but isn't actually equal to 1. So if we take n large enough, the probability of failure will eventually converge to 0; meaning that with high probability we will have at some point succeeded in producing The Hobbit. It's not clear what's meant by an event being "probable," but if, say, we wanted there to be a 95% probability of success, meaning a 5% chance of failure, we would need . So to solve for n, we can take logarithms of both sides and divide by , to get that , which is on the order of , or about blocks of characters.

6.) To give you a sense of how incredibly large this number is, if we generated 200 characters per second, as you say, then 360,000 characters would take 30 minutes, so we could produce about 48 new blocks every day, or 17650 per year, on the order of . This would mean that our blocks would take about years. For comparison, the universe is estimated to be around 13 billion years old, approximately , so you would need ages of the universe to have completed the task with 95% probability. Even if you had every atom in the universe working in parallel for the lifetime of the universe, you'd barely make a dent. Surely all our protons would have decayed into nothingness long before you even got to the part in the book where the trolls get turned to stone.

I suppose the moral of all of this, if you believe in that sort of thing, is that sometimes the mathematical consequences of our assumptions can far outstrip our intuition, especially when it comes to events that are exceedingly rare or numbers that are exceedingly large. So in a sense your "gut feeling" is right as far as any practical considerations go. Jorge Luis Borges wrote a story about this called The Library of Babel, which deals exactly with your scenario of a powerful being producing every possible book of a certain length. It's true that among such a vast library, there would be a comprehensive volume of the history of tea-drinking. However, there would also by necessity be an incredible number of false histories, every possible one in fact, as well as fraudulent cures for cancer and incorrect predictions for the next 100 World Series winners, and, importantly, there would be no way to distinguish the fake from the genuine. So it's back to option (a) I'm afraid--just write the book.

-DrM

In the Big Apple, I prefer Honeycrisp.

I've been called out by Short Round over at alt85 again, concerning a recent article in The New York Times:

The article included one piece of information with direct relevance to the little people: "a new study from the Center for an Urban Future, a nonprofit research group in Manhattan, estmates that it takes $123,322 to enjoy the same middle-class life as someone earning $50,000 in Houston." [Tugs nervously at collar.] And since the average median* per-capita income in Houston in 1999 (according to houstontx.gov) was $20,101, and since the Urban Future people's figures would suggest that $20,101 in Houston is worth less than $49,578 in New York (for reasons that the newly returned Dr. Math could surely explain better than I,** unless he disagrees, in which case I challenge him to a duel)... Well, New York is f**kin' expensive. Not news.
Short Round

Sir, I accept!

So, I'm not generally opposed to the conclusion that New York ¢ity is an expensive place to live. (God knows I could use an extra $500K a year to spend on all those things that I've heard the city is supposedly famous for but that I'm too poor to experience.) The authors of this article seem to be basically assuming that conclusion from the beginning. In a sense, all this "news" piece is even claiming to do is put some quantitative weight behind a stereotype that we've all pretty much agreed on already. But since it involves numbers, I can't resist picking apart their methodology a little. The Devil, as always, is in the details:

First off, I had to do some considerable digging to even get to the original source of this email-forward-ready statement that $50,000 Houston dollars is equivalent to $123,322 Dollars New York ($NY). The Times article cites a report from the oddly-named Center for an Urban Future, which used a cost-of-living calculator from the CNN (yes, CNN) website, which had as its source material a survey done by the Council for Community and Economic Research (C2ER), in which they hired surveyors to sample prices from various cities they wanted to compare (more on that later). The (Center for an Urban Future) report is a 52 page document entitled "Reviving the City of Aspiration" about ongoing trends in the middle class of America, particularly in New York. One problem right off the bat is that the authors never precisely define what they mean by "middle class". They write, "In this study, we use ['middle class'] to indicate those who own homes or who have the prospect of becoming homeowners, earn at least in the middle quintile of wages and enjoy a modicum of economic stability." They then go on to wax poetic for a while about the important contributions middle class Americans make to society (including "providing the customer base for a wide mix of businesses across the city," adding to New York's "street life" and, somewhat circularly, owning homes). But setting aside the logical hiccup for a minute, it's still not clear from the definition who exactly qualifies as middle class. Rather, it's somewhat clear what the minimum standards are for membership--you have to own a home or have "the prospect" of doing so, earn "at least in the middle quintile of wages," which is sloppily phrased but I'm guessing means you have to earn more than at least 40% of people in the area, and have "a modicum" of economic stability, which they explain as being able to consistently pay your bills--but there seems to be no clear maximum standards. For example, would someone earning $250K per year in the 98th percentile be considered middle class, assuming he owned a house and could pay his bills (for monocle cleaning and storage)? Maybe, by the authors' definition, but certainly not by mine.

Now, if we trace this comparison-of-cities data all the way back to its source, the C2ER survey, we find an interesting disparity. The basic idea of the survey was to follow some sample of people around and make a log of the prices of all the things they paid for--clothes, food, entertainment, travel, etc.--to get a measurement of the relative cost of living in different places. However, in the guidelines for the survey participants, it says specifically that the authors are not looking for middle class consumers to follow around (they changed their original survey language because "it was too easily confused with 'middle class,' which isn't the same thing at all"); rather, they focus on a population they call "moderately affluent professional and managerial households", who are characterized as "a household consisting of both spouses and one child (for pricing apartments, it is assumed that the couple is childless or the individual is single)" with the criteria that "both spouses hold college degrees; at least one has an established professional or managerial career," and, most significantly, "household income is in the top quintile for the area" (emphasis mine). For most cities, they say that the household annual income should be "between $70,000 and $100,000;" however, as they say, "the appropriate income range will be higher in traditionally high-cost places like New York..." So our monocle-polishing Uncle Moneybags the hedge fund manager would be included in the survey.

What's the real problem with this? Apart from the fact that we've gotten, explicitly, pretty far away even from the ill-defined "middle class" of the Urban Future report, upon whose homeowning backs the street life of the city rests, we've also gotten into some shaky statistical territory, where I believe we're not even comparing apples to apples anymore, but rather something like apples to different kinds of apples (Fuji to Jonagold), to learn all about oranges. And also the middle class. I don't have any hard data to back me up here, but my sense from having lived in New York for a little while now is that, due to the presence of so many ultra rich celebrities and financiers, the shape of the distribution of incomes here is more heavily slanted towards the top ("fat-tailed," as they say), meaning not only is the average income higher, but the relative difference between the top 20% and those of us way down in the middle is considerably greater than in other U.S. cities. In pictures, the graph of incomes in New York is more like this:















than this:


















In the latter case (Houston), it doesn't take much more income to put you in the top 20%, but in New York, it takes considerably more. So, the potential gap in luxury lifestyles is exaggerated, and as a result, more especially luxurious opportunities open up for those who can afford them. There really just isn't a Houston equivalent of buying a $150 truffle and foie gras burger at Bistro Moderne or paying $75K per year for a personal driver or all the other outrageous things the Times article mentions.

Which all brings me all the way around to the point: that measuring what it costs to uphold a "standard of living" is an extremely difficult and subtle problem, one which requires a great deal of precision and care. And it may not really be possible when the markers of that standard vary so greatly from place to place. New York is a pretty special town with no real equivalent anywhere else in the U.S., and in fact, based on the ways we live our lives, renting instead of owning, riding the subway instead of driving, eating fancy burgers made out of goose liver... it may not even make sense to think of it as part of the U.S., despite its importance as a cultural hub.

Like the old song goes, "New York, New York, it's a pretty special town with no real equivalent anywhere else in the U.S., and in fact, based on the ways we live our lives, renting instead of owning, riding the subway instead of driving, eating fancy burgers made out of goose liver... it may not even make sense to think of it as part of the U.S., despite its importance as a cultural hub."

-DrM


P.S.--To Short Round: oddly enough, it seems that "average median" is correct there. In the report, they averaged together the median incomes of the various ethnic groups in the suburbs of Houston, presumably with some weighting. Hence, average median income. Weird.

The Scales of Justice

Dear Dr. Math,
I don't mean to be crass, but what are the chances that Ruth Bader Ginsburg is going to die during Barack Obama's presidency? I read that the average lifespan of an American is 78 years, and she's only 75 but now she has cancer. Also, some of the other judges are old, too. How many appointments is he probably going to have to make in the next 4 years?
Sincerely,
ScotusLover728

Dear ScotusLover,

With the recent news about Justice Ginsburg being diagnosed with pancreatic cancer, this is a topic on the minds of a lot of people. Of course, we're all hoping for the best for her, but the issue of Supreme Court appointments has ramifications far beyond our wishes for her health. When one vote can make the difference in who can stick what in whose what or whether little old ladies deserve equal pay for equal work or even who the president was for the last 8 years, the news that one of the justices has a potentially deadly illness gets everyone's attention.

First off, we should dispense with the whole "average lifespan" argument, which is largely irrelevant here. The statistics you've probably seen quoted are the expected (in the sense of average, or mean) lifespan of someone born today. It includes the effect of a fair number of people dying young. As someone gets older, his/her expected lifespan increases, because we have to incorporate into the calculation the fact that he/she is still alive. The relevant numbers for these things can be found in what are called life tables, which are tools that actuaries use to figure out what your grandmother's life insurance premiums should be, etc. However, these are still just averages over large swaths of the population and they don't take into consideration any more particular information we might have about someone.

So, in Justice Ginsburg's case, the more relevant number is the mortality rate for her particular form of pancreatic cancer, given the stage at which it was diagnosed. And unfortunately, the numbers are not particularly good. One number that the news media seems to have latched onto is that only 5% of people diagnosed with pancreatic cancer survive for 5 years after the diagnosis. Again, I'm not a doctor, but from Googling around I've discovered that a big part of the reason pancreatic cancer is so deadly is that it frequently goes undetected until it's already in a fairly advanced stage. So, the fact that her cancer was caught relatively early should work to her favor. I think the right number to be considering here is the survival rate for pancreatic cancer in its earliest stage, which is something like 35% after 5 years.

It's important to remember, also, that these statistics just reflect the potential of dying from the disease (assuming they're measuring relative survival rates). That is, the number 35% is supposed to represent the percentage of people diagnosed with cancer who are still alive after 5 years given that they would have been alive anyway. Of course, it's a difficult thing to measure, but it means we should include the fact that Ruth is 75 years old and that just being 75 itself has a 5 year survival rate of 83% (for American females). To determine that overall survival rate, I took the number of women alive at age 80 and divided by the number alive at age 75.

In the final tally, then, my best guess for Justice Ginsburg's chances of living out the next 5 years would be the chance that any 75-year-old woman would live 5 more years times the relative survival rate for someone with an early diagnosis of pancreatic cancer, that is, (.83)*(.35) = .29, or 29%. There's no accounting for determination, the will to live, or hatred of Antonin Scalia, however. The lesson to draw from all of this is that the more information you have about a particular person, the more precisely you can fine-tune the analysis of his/her situation, but also the less data you have to draw conclusions from. Really, what we'd like to know is the 5 year survival rate for being Ruth Bader Ginsburg, but there's only been 1 known case in history.

To answer your other question about likely Supreme Court appointments, I could go through each remaining justice and compile mortality tables for each based on his particular lifestyle and risk factors, but maybe I should leave that as an exercise for the reader. Personally, I find all this kind of creepy. I will say that Justice Stevens is 88, and the 5 year survival rate for an 88-year-old American male is 36%, or about the same as Justice Ginsburg's cancer diagnosis. Of course, there can be many reasons for a justice to leave the court besides death, as well. Of the 101 Supreme Court justices who have left the court, only 50 have done so by dying. The remaining 51 resigned or retired, presumably before they died, unless they were pulling a Jeremy Bentham. It appears that having an extremely silly name is not a risk factor.

A rough estimate for the average rate of appointments can be gotten by dividing the total number of appointments, 110, by the age of the Supreme Court, which is 220 years young (happy birthday, Supreme Court!). So that's a rate of about half a justice per year, meaning Barack Obama will have to appoint an average of 2 justices for each term he serves as president.

-DrM