Tuesday, October 7, 2008
Rods to the Hogshead
Dear Doctor Math,
Should I buy a Prius or a Honda Civic? At the Toyota dealership they told me the Prius pays for itself in gas savings, but I don't trust them.
Thanks,
Deke
Well, Deke, it's good to be skeptical. But let's see if we can crunch the numbers and settle this for ourselves without having to trust a car salesman to figure it out for us.
First, we'll have to make some assumptions about the costs of the various things in question and the ways that you're planning to use your car, whichever one you get. All of the numbers I'm about to quote came from the EPA's fuel economy website. Now, I don't know anything about you, but I'll go ahead and assume you drive about 15,000 miles per year, like the average American does. (Someday I'll write about the difference between "average" and "typical," but we'll table that discussion for now.) Of that 15,000 miles, I'll assume that approximately 55% is "city" driving and the other 45% is "highway," again in keeping with the average. So that works out to 8,250 miles in the city and 6,750 miles on the highway. If you're involved in a lot of cannonball runs, you can adjust accordingly.
According to the EPA's latest numbers, the 2009 Honda Civic gets 25 miles per gallon in the city, 36 highway. So, every year you would use 8,250/25, or 330, gallons of gas in city driving and 6,750/36, or 187.5, gallons on the highway. You total volume of gas used per year in the Civic would be 330 + 187.5, or 517.5 gallons.
Due to its greater efficiency in stop-and-go traffic, the Toyota Prius gets 48 miles per gallon in the city and 45 on the highway. Therefore, the total amount it guzzles per year is 8,250/48 + 6,750/46, or 321.8 gallons.
Now, gas prices are hard to predict, but let's guess that over the lifespan of your car, gas will cost an average of $4.00 per gallon (in 2008 dollars). That seems like a reasonable projection given the way prices have historically risen. So that works out to 517.5*4, or $2,070, per year for the Civic and 321.8*4, or $1,287, for the Prius. Every year, that means you save $783 by driving the Prius.
According to the manufacturers, the suggested retail price for the Civic is $16,205; for the Prius it's $22,000. These prices assume a basic package; probably, any extras you might want, like ground effects or those things that make it jump up and down, would cost about as much for either car. The difference in price, therefore, is $5,795, which would take 5,795/783, or about 7.4, years to pay off in gas savings. Of course, if gas goes up even more, say to $5 per gallon, that number would come down to as little as 6 years.
Either way, it seems like a fairly long time, but not outside the realm of possibility. I couldn't find any good numbers here, but people I know who own cars seem to get a new one about every 5 years. Maybe you hold to your cars a little longer, Deke, or maybe there might be other things about driving a Prius that appeal to you, I don't know. But strictly in terms of the gas savings, it doesn't seem to quite be worth it, although it's close. The market seems to have done a pretty good job sorting out these relative prices.
An interesting side-note here is that the marginal gas savings (that is, the money saved per every additional mpg) go down as the cars get more efficient. For example, doing the same calculation as before, we can see that an SUV that gets 10 miles per gallon costs $1,000 more per year in gas than one that gets 12 miles per gallon. So, the more important choices may not be between pretty good and very good, but between bad and very-slightly-less-bad.
-DrM
Sunday, October 5, 2008
Poll Position
Dear Doctor Math,
I saw a poll today that said Obama is up 7 percentage points in Ohio with a margin of error of 4%. So does that mean he could actually be losing there? Also, how can they come up with these numbers just by asking a few hundred people?
A Concerned Citizen
Those are good questions, ACC, and they're related. To answer them, I should talk a little about how polling works and what the various numbers mean. First off, polling is an imperfect attempt at predicting the future. No one knows for sure what's going to happen on election day, and sometimes (see Florida in 2000) it's hard to figure out what did happen even after the election. But polls are our best guess, and usually they do a pretty good job.
To conduct a poll, a news agency like CBS or Reuters or a public opinion firm like Rasmussen gets a staff of questioners to each call a handful of people and ask them their opinion on things, like how they're planning to vote. Since it takes time and money to make the calls, the pollsters typically limit themselves to something like a few thousand people. Of course, a lot of people (like young people who don't have landlines and probably vote Democratic, but never mind...) don't answer, so by the time the pollsters compile all their data together, they've got maybe 1000 quality responses to go on. From here they try to figure out what the remaining millions of people in the state or country are thinking, and then they report that information, thereby influencing the way people think, but that's another story.
So, the first question is, how do they know they didn't just ask all the wrong people? And the answer is they don't know for sure, of course, but if their methods are sound they can say with a reasonable degree of certainty that their polling numbers reflect the larger population. Think of Mario Batali tasting a single spoonful out of a pot of marinara sauce to see if it needs more oregano. Of course, it's possible he just got the most oreganoed spoonful in the whole pot, but if he's done a good job of stirring it up beforehand, he can be reasonably sure that his sample was representative of the distribution of the whole. But it would still be embarrassing for him to be wrong, so it would be nice to at least have some idea how much of a risk he was taking or maybe if he should taste it again.
That's where the "margin of error" comes in. The error that pollsters give is an indication of how sure they are that the sample they chose is a reasonable reflection of the population at large. For reasons I hope to get into someday (involving The Central Limit Theorem), the pollsters assume that the "true" value of the thing they're estimating follows a bell-shaped curve centered around their estimate. So, if they're trying to figure out how many people in Ohio are going to vote for Obama, they take the results from their poll (49% in the latest Columbus Dispatch poll) and say that the actual percentage of people planning to vote for Obama has a probability distribution forming a bell-curve centered around 49%. That means they can actually quantify the probability that their estimate is off by any given amount. The margin of error is the amount of deviation it takes before the pollsters can say with 95% probability that the true value is within that much of the estimate. They pick 95% mostly out of convention and the fact that it's easy to compute. Here, the key factor is the number of respondents--a rough formula for the margin of error (at the 95% level) for a sample of N people is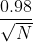
, which for 1000 people comes out to be about 0.03, or 3%. They might occasionally bump it up to 4% just to be extra sure.
Now, to answer your question, does this mean that McCain could actually be ahead? After all, the 7 point difference is less than twice the margin of error, so if we add that much to McCain and take it away from Obama, it does put McCain on top. It's possible, as I mentioned above, that the pollsters just asked enough of the wrong people to skew the numbers. In fact, if you've been paying close attention to what I said about the true value having a bell-curve distribution, you might have noticed that actually the situation is in some sense worse than just that. That 4% number is just the cutoff for the 95% confidence interval; it could be (with about 5% probability) that the poll is off by even more than 4%. Should we just throw up our hands and quit?
The important thing to remember here is that the margin of error isn't the end of the story. The bell-shaped curve which gave us the error calculation also shows us that it's more likely than not that our estimate is close to the truth. So again, we can quantify the degree of certainty that we have in estimating the difference between Obama's percentage and McCain's. Using a formula (that I admit I had to look up), we can compute that the standard error, a measure of how spread out the distribution is, in that estimation of the 7% Obama-McCain gap in Ohio is about 0.03. That means the bell-curve is pretty narrowly distributed around the guess. According to the bell-curve distribution, this gives a probability of about 99% that Obama is "truly" ahead in Ohio.
So, yes, even if those polling numbers are correct, it is possible that McCain's ahead, but I wouldn't bet on it (unless someone was giving me greater than 100-to-1 odds).
-DrM
I saw a poll today that said Obama is up 7 percentage points in Ohio with a margin of error of 4%. So does that mean he could actually be losing there? Also, how can they come up with these numbers just by asking a few hundred people?
A Concerned Citizen
Those are good questions, ACC, and they're related. To answer them, I should talk a little about how polling works and what the various numbers mean. First off, polling is an imperfect attempt at predicting the future. No one knows for sure what's going to happen on election day, and sometimes (see Florida in 2000) it's hard to figure out what did happen even after the election. But polls are our best guess, and usually they do a pretty good job.
To conduct a poll, a news agency like CBS or Reuters or a public opinion firm like Rasmussen gets a staff of questioners to each call a handful of people and ask them their opinion on things, like how they're planning to vote. Since it takes time and money to make the calls, the pollsters typically limit themselves to something like a few thousand people. Of course, a lot of people (like young people who don't have landlines and probably vote Democratic, but never mind...) don't answer, so by the time the pollsters compile all their data together, they've got maybe 1000 quality responses to go on. From here they try to figure out what the remaining millions of people in the state or country are thinking, and then they report that information, thereby influencing the way people think, but that's another story.
So, the first question is, how do they know they didn't just ask all the wrong people? And the answer is they don't know for sure, of course, but if their methods are sound they can say with a reasonable degree of certainty that their polling numbers reflect the larger population. Think of Mario Batali tasting a single spoonful out of a pot of marinara sauce to see if it needs more oregano. Of course, it's possible he just got the most oreganoed spoonful in the whole pot, but if he's done a good job of stirring it up beforehand, he can be reasonably sure that his sample was representative of the distribution of the whole. But it would still be embarrassing for him to be wrong, so it would be nice to at least have some idea how much of a risk he was taking or maybe if he should taste it again.
That's where the "margin of error" comes in. The error that pollsters give is an indication of how sure they are that the sample they chose is a reasonable reflection of the population at large. For reasons I hope to get into someday (involving The Central Limit Theorem), the pollsters assume that the "true" value of the thing they're estimating follows a bell-shaped curve centered around their estimate. So, if they're trying to figure out how many people in Ohio are going to vote for Obama, they take the results from their poll (49% in the latest Columbus Dispatch poll) and say that the actual percentage of people planning to vote for Obama has a probability distribution forming a bell-curve centered around 49%. That means they can actually quantify the probability that their estimate is off by any given amount. The margin of error is the amount of deviation it takes before the pollsters can say with 95% probability that the true value is within that much of the estimate. They pick 95% mostly out of convention and the fact that it's easy to compute. Here, the key factor is the number of respondents--a rough formula for the margin of error (at the 95% level) for a sample of N people is
Now, to answer your question, does this mean that McCain could actually be ahead? After all, the 7 point difference is less than twice the margin of error, so if we add that much to McCain and take it away from Obama, it does put McCain on top. It's possible, as I mentioned above, that the pollsters just asked enough of the wrong people to skew the numbers. In fact, if you've been paying close attention to what I said about the true value having a bell-curve distribution, you might have noticed that actually the situation is in some sense worse than just that. That 4% number is just the cutoff for the 95% confidence interval; it could be (with about 5% probability) that the poll is off by even more than 4%. Should we just throw up our hands and quit?
The important thing to remember here is that the margin of error isn't the end of the story. The bell-shaped curve which gave us the error calculation also shows us that it's more likely than not that our estimate is close to the truth. So again, we can quantify the degree of certainty that we have in estimating the difference between Obama's percentage and McCain's. Using a formula (that I admit I had to look up), we can compute that the standard error, a measure of how spread out the distribution is, in that estimation of the 7% Obama-McCain gap in Ohio is about 0.03. That means the bell-curve is pretty narrowly distributed around the guess. According to the bell-curve distribution, this gives a probability of about 99% that Obama is "truly" ahead in Ohio.
So, yes, even if those polling numbers are correct, it is possible that McCain's ahead, but I wouldn't bet on it (unless someone was giving me greater than 100-to-1 odds).
-DrM
Saturday, October 4, 2008
Fallacy of the Week: The Base Rate Fallacy
Dear Doctor Math,
If a doctor tells you that you tested positive for something and that the test is 99% accurate, does that mean you have a 99% chance of having the disease? Just curious.
MTG
I should probably begin by reiterating that I'm not actually a doctor, at least not that kind (see earlier post), so please don't take what I'm about to say as medical advice. But basically the answer is no, or at least you can't tell without further information. You see, what your doctor may have omitted telling you is the base rate for the disease in question, that is, the general probability of having the disease without the extra information that you tested positive for it. If that base rate is really low, even a very accurate test isn't a strong indicator of having the disease. Let me illustrate with some numbers:
Let's say that, on average, 1 out of every 1 million people suffers from psychogenic dwarfism. So, for this condition your base rate is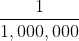
, or .0001%. Now, you go in for a physical and the doctor says that you tested positive for this debilitating condition, and that the test is 99% accurate. There's some room for interpretation as to what that means exactly, but let's take it to mean that (1) if you actually have the condition, you'll definitely test positive, and (2) if you don't have the condition, there's a 99% chance you'll test negative. So, what are your odds? Well, imagine that 100 million people go in for tests. We know that about 100 of them will actually be psychogenic dwarves. Of the remaining 99,999,900 people, however, about 1% will test positive even though they don't have it. So that means 999,999 false positives compared to only 100 true positives. The total number of people testing positive is 100 + 999,999, or 1,000,099, and only 100 of them actually have the disease. Since all you know is that you tested positive, you don't know which of these people you are, so your chance of actually being positive is 
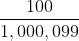, about 1 in 10,000, or .01%. Bottom line: it's still very unlikely that you have the condition, even though you tested positive for it and the test is very accurate, so don't go out and sell all your normal-sized clothes just yet.
The basic rule here is always to consider the number of true positives relative to the total number of people who would test positive, true or false. What we've seen in this example, and what frequently turns out to be the case, is that even a test that sounds like a sure thing can end up producing way more false positives than true ones, just because there aren't that many true positives out there to discover. (For another example, ask the Department of Homeland Security about their terrorist-detecting techniques.) I think part of the problem here is that we're dealing with numbers that we don't have much intuitive grasp for. I mean, "one in a million" basically means it won't ever happen, right? But "99 percent accurate" means it must be true. So how do you decide? The nice thing about math is that can't get bullied around by intimidating sounding numbers like these; it just puts them in their relative place. Remember, probability is ultimately all about information, and it should take a lot of evidence to convince us of something extremely unlikely.
-DrM
If a doctor tells you that you tested positive for something and that the test is 99% accurate, does that mean you have a 99% chance of having the disease? Just curious.
MTG
I should probably begin by reiterating that I'm not actually a doctor, at least not that kind (see earlier post), so please don't take what I'm about to say as medical advice. But basically the answer is no, or at least you can't tell without further information. You see, what your doctor may have omitted telling you is the base rate for the disease in question, that is, the general probability of having the disease without the extra information that you tested positive for it. If that base rate is really low, even a very accurate test isn't a strong indicator of having the disease. Let me illustrate with some numbers:
Let's say that, on average, 1 out of every 1 million people suffers from psychogenic dwarfism. So, for this condition your base rate is
The basic rule here is always to consider the number of true positives relative to the total number of people who would test positive, true or false. What we've seen in this example, and what frequently turns out to be the case, is that even a test that sounds like a sure thing can end up producing way more false positives than true ones, just because there aren't that many true positives out there to discover. (For another example, ask the Department of Homeland Security about their terrorist-detecting techniques.) I think part of the problem here is that we're dealing with numbers that we don't have much intuitive grasp for. I mean, "one in a million" basically means it won't ever happen, right? But "99 percent accurate" means it must be true. So how do you decide? The nice thing about math is that can't get bullied around by intimidating sounding numbers like these; it just puts them in their relative place. Remember, probability is ultimately all about information, and it should take a lot of evidence to convince us of something extremely unlikely.
-DrM
Thursday, October 2, 2008
Boys and/or Girls
Here's a classic probability puzzler that's been floating around in the aether recently. The particular question came from my good friend Short Round over at www.alt85.com:
Dear Doctor Math,
You know that a certain family has two children, and that at least one is a girl. But you can't recall whether both are girls. What is the probability that the family has two girls? I stole this question from the infernet.
SR
First let me give the answer, and then I'll talk about why it sounds wrong.
The answer is
. Let's call the two kids Ashley and Whitney (could be boys' or girls' names, get it?); there are initially four possibilities for the genders of (Ashley, Whitney) without the extra restriction that one has to be a girl. They are: (boy, boy), (boy, girl), (girl, boy), (girl, girl). Assuming that each kid is a boy or a girl with equal probability and that the genders of the kids are independent from each other, each pairing has probability 
because we have no information to prefer one over the others. Now, with the added information that at least one is girl (we saw some moisturizer in the bathroom but we don't know whose it is), we can eliminate the (boy, boy) possibility. However, we still have no information to indicate that any one of the remaining three pairings is more likely than any other, and so the probability of each of them is , given the new information. Thus, the chance of there being two girls is .
Now, as I mentioned before, this is a classic brainteaser, which really just demonstrates the weird counterintuitive things that can happen when you ask for the probability of an event given some unusual information. Most people balk at the idea of there being a
chance of a kid being a boy, because they're so conditioned to think of the odds always being equal, but since probability is an expression of the information you have about some event and the consequences of said information, it's entirely possible to construct bizarre examples like this one (it's hard to contrive a scenario where you would know just that one of the kids is a girl but not know which one). Strangely, if you know the oldest child is a girl, then the probability of the other being a girl goes back up to 
.
To show what would happen if you took this a few steps further--let's say you had a whole busload full of 10 people with androgynous names and you didn't know the genders of any of them. To help us tell them apart, let's refer to each by his/her seat number, 1 through 10. There are two possibilities for each person, and they're independent of each other, so to start off with, there are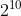
, or 1024, possible configurations for the gender line-up, all equally likely. Now, suppose you find Zac Efron posters in the duffel bags of nine out of the ten people, so you know there are at least nine girls but somehow you don't know who they are. Given that information, you can eliminate all but 11 remaining possibilities: either they're all girls, or there's one boy, and he's sitting in one of 10 possible seats. Again, we have no reason to think one of these outcomes is more likely than any other; thus, the resulting probability that you actually have a bus full of all girls is 
.
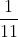Like puberty, probability can be scary sometimes, but that's just life.
-DrM
Dear Doctor Math,
You know that a certain family has two children, and that at least one is a girl. But you can't recall whether both are girls. What is the probability that the family has two girls? I stole this question from the infernet.
SR
First let me give the answer, and then I'll talk about why it sounds wrong.
The answer is
Now, as I mentioned before, this is a classic brainteaser, which really just demonstrates the weird counterintuitive things that can happen when you ask for the probability of an event given some unusual information. Most people balk at the idea of there being a
To show what would happen if you took this a few steps further--let's say you had a whole busload full of 10 people with androgynous names and you didn't know the genders of any of them. To help us tell them apart, let's refer to each by his/her seat number, 1 through 10. There are two possibilities for each person, and they're independent of each other, so to start off with, there are
Like puberty, probability can be scary sometimes, but that's just life.
-DrM
We all use math every day. Or do we? Yes.
Hi and welcome to Ask Doctor Math, the warm cozy corner of the Internet where anyone with a math question can pull up a virtual seat, grab a mug of hot virtual cocoa, and sit by the glowing virtual fire of knowledge as I attempt to answer questions mathematical. I created this blog as a forum for people young and old to clear up some lingering misconceptions, bring fuzzy notions a little more into focus, and, with luck, add a few more tools to the toolbox of ideas they use to make sense of the world. I may not be that kind of doctor, but I'd like you to think of me that way anyway--the friendly old small-town physician you can come to with anything, from questions about birth control or that rash on your back to home remedies for a colicky baby or a toothache; hell, I'll even help birth a foal, if that's what you need. (Note: the preceding was just an extended metaphor.) I hope to be your guide on a journey of mathematical discovery. So please, come on in and make yourself at home. Take off your virtual shoes if you like, or don't, it's up to you.
To kick things off, I thought I'd reply to a question that seems to be on a lot of people's minds these days regarding the alleged difference between the "mathematical world" and the so-called "real world."
Dear Doctor Math,
A guy on TV keeps telling me that "We all use math every day." Is that really true? Give several dozen examples.
Sincerely,
Dr. Math (you)
Before even beginning to scratch at the surface of that question, I think we should talk a little about what we mean by "math" exactly. For a lot of people I've talked to, "math" is basically synonymous with "numbers." So, in that sense, yes, we probably do all encounter math every day, telling time, riding on a bus, dialing a phone, etc. If we didn't have numbers, we'd be forced to use little pictures of things, so it's convenient to have a shorthand. But a lot of that could only be superficially described as mathematical.
Perhaps a little more tangible application of math is in quantitative reasoning--the kind of thing we're forced to do a lot in our capitalistic society ("How much is 30% off $80?", "How do I split a $32 dinner bill 3 ways?", "Which is a better value, a 2'x3' rug for $25 or a 4'x6' rug for $60?", "How long will it take me to go 90 miles if I average 55 miles per hour?", "How many fluid ounces are in 2.5 liters?", etc.). The main tools we generally use here are fractions, percents, ratios, and basic arithmetic--addition, subtraction, multiplication (and its evil stepchild division). A lot of the time we just ballpark it, though, and our powers of guesstimation are more or less adequate to get us through a typical day. When it's really important that we get something right, we outsource the job to a computer, cell phone, calculator, or cash register. So in that sense, I'd say we use math, but we could probably all stand to be a little better at it. At any rate, there's not much genuine thinking involved.
Probably what the writers of Numb3rs had in mind, though, is the notion (championed by high school math teachers everywhere), that even when we're not explicitly dealing with numbers (or numb3rs), we frequently use our powers of analytical reasoning in a way that could be broadly be considered mathematical. Our toolkit here includes such things as deductive logic ("Just because I said that dress doesn't make you look fat doesn't mean you don't.", "Every girl knows someone who likes everyone else more than her."), elementary hypothesis testing ("My doctor said the test is 90% accurate; how concerned should I be?", "I guess there could be an innocent explanation for why that guy would be running down the street carrying a TV at 2am." ), and management of risk ("What does it mean that my birth control method is 99.9% safe?", "The weather forecast calls for a 30% chance of rain; should I bring an umbrella or not?"). I would also include in this category some basic optimization problems, like "How do I fit all these boxes in the car?", "Is this couch too big to fit through my hallway?", or "Should I park here or look for a better spot?". Again, these questions don't really tap our quantitative skills so much as our rational/logical thinking skills. A lot of it is intuitive, but a lot can be trained by thinking our way through other rational/logical problems. At its core, that's what math is really all about--practice for the kind of problem-solving that's required of us to navigate a sometimes complex and baffling world.
And like it or not, we are being subjected to persuasion of an increasingly mathematical bent. News reports like clockwork regularly tell us what activities or foods might be correlated with cancer or aging. As we move into political crunch-time, we are barraged almost daily by statistical arguments about the state of the nation and who might be to blame for what, as well as the frequent polling results with their "margins of error" and what this means for the so-called "electoral math." The present crisis on Wall Street has, among other things, shown the hazard in trusting all of our quantitative risk-management to a few experts, whom we treat like the high priests who are the only ones allowed into the holy sanctuary. If we're afraid to take responsibility for our role in distinguishing mathematical argument from fallacy, we will only get more and more manipulated by those to whom we yield that authority.
In other words, we may not use math every day, but it sure as hell uses us.
-DrM
To kick things off, I thought I'd reply to a question that seems to be on a lot of people's minds these days regarding the alleged difference between the "mathematical world" and the so-called "real world."
Dear Doctor Math,
A guy on TV keeps telling me that "We all use math every day." Is that really true? Give several dozen examples.
Sincerely,
Dr. Math (you)
Before even beginning to scratch at the surface of that question, I think we should talk a little about what we mean by "math" exactly. For a lot of people I've talked to, "math" is basically synonymous with "numbers." So, in that sense, yes, we probably do all encounter math every day, telling time, riding on a bus, dialing a phone, etc. If we didn't have numbers, we'd be forced to use little pictures of things, so it's convenient to have a shorthand. But a lot of that could only be superficially described as mathematical.
Perhaps a little more tangible application of math is in quantitative reasoning--the kind of thing we're forced to do a lot in our capitalistic society ("How much is 30% off $80?", "How do I split a $32 dinner bill 3 ways?", "Which is a better value, a 2'x3' rug for $25 or a 4'x6' rug for $60?", "How long will it take me to go 90 miles if I average 55 miles per hour?", "How many fluid ounces are in 2.5 liters?", etc.). The main tools we generally use here are fractions, percents, ratios, and basic arithmetic--addition, subtraction, multiplication (and its evil stepchild division). A lot of the time we just ballpark it, though, and our powers of guesstimation are more or less adequate to get us through a typical day. When it's really important that we get something right, we outsource the job to a computer, cell phone, calculator, or cash register. So in that sense, I'd say we use math, but we could probably all stand to be a little better at it. At any rate, there's not much genuine thinking involved.
Probably what the writers of Numb3rs had in mind, though, is the notion (championed by high school math teachers everywhere), that even when we're not explicitly dealing with numbers (or numb3rs), we frequently use our powers of analytical reasoning in a way that could be broadly be considered mathematical. Our toolkit here includes such things as deductive logic ("Just because I said that dress doesn't make you look fat doesn't mean you don't.", "Every girl knows someone who likes everyone else more than her."), elementary hypothesis testing ("My doctor said the test is 90% accurate; how concerned should I be?", "I guess there could be an innocent explanation for why that guy would be running down the street carrying a TV at 2am." ), and management of risk ("What does it mean that my birth control method is 99.9% safe?", "The weather forecast calls for a 30% chance of rain; should I bring an umbrella or not?"). I would also include in this category some basic optimization problems, like "How do I fit all these boxes in the car?", "Is this couch too big to fit through my hallway?", or "Should I park here or look for a better spot?". Again, these questions don't really tap our quantitative skills so much as our rational/logical thinking skills. A lot of it is intuitive, but a lot can be trained by thinking our way through other rational/logical problems. At its core, that's what math is really all about--practice for the kind of problem-solving that's required of us to navigate a sometimes complex and baffling world.
And like it or not, we are being subjected to persuasion of an increasingly mathematical bent. News reports like clockwork regularly tell us what activities or foods might be correlated with cancer or aging. As we move into political crunch-time, we are barraged almost daily by statistical arguments about the state of the nation and who might be to blame for what, as well as the frequent polling results with their "margins of error" and what this means for the so-called "electoral math." The present crisis on Wall Street has, among other things, shown the hazard in trusting all of our quantitative risk-management to a few experts, whom we treat like the high priests who are the only ones allowed into the holy sanctuary. If we're afraid to take responsibility for our role in distinguishing mathematical argument from fallacy, we will only get more and more manipulated by those to whom we yield that authority.
In other words, we may not use math every day, but it sure as hell uses us.
-DrM
Subscribe to:
Posts (Atom)
