How Big is That Number? Episode 1

This will be the first installment of a new feature I call "How Big is That Number?" in which I try to explain exactly how big that number is.

Dear Dr. Math,
How much space would a googol grains of sand take up?
xoxo,
Frequent Googol Searcher

Dear FreGooSear,

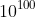
Let me begin by thanking you for reminding us all of the correct spelling of "googol". A lot of people forget that before it inspired the name of an obscure website, the word "googol", as coined by a man named Milton Sirotta back in 1938, referred to the number . I don't know the whole story here, but I'm guessing that as an infant, he somehow wrote a 1 followed by 100 zeroes (I'm guessing in blue crayon), and when asked by his parents what that was, all he could make were baby sounds. Hence the name. Any other explanation seems highly improbable.

So, how big is this number with the silly name? Well, first off, if we wanted to address it in the nomenclature of billions and trillions, it would be known as ten thousand trillion trillion trillion trillion trillion trillion trillion trillion. That's a ten-thousand followed by 8 trillions. Or, if you prefer to think of it in terms of current financial events, $1 googol would be about 12,706 trillion trillion trillion trillion trillion trillion trillion economic stimulus packages.

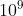
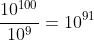
Now, to answer your question about grains of sand: let's approximate a grain of sand as a cube 1 millimeter across. That would mean that 1000 grains of sand in a row would be 1 meter long. So, one cubic meter would contain 1000*1000*1000, or , grains. A googol grains, therefore, would take up cubic meters of space. And it would really be "space", because this is way bigger than our tiny little planet could accommodate. 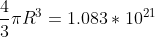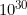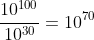For comparison, a sphere the size of the Earth (which has a radius of about 6,371 kilometers, or 6,371,000 meters) has, according to the formula for the volume of a sphere, a volume equal to cubic meters, about grains of sand, so it would take about Earth-sized balls of sand to get a googol grains. 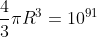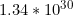Alternatively, if you lumped all the sand together into one giant ball, you'd need cubic meters, and solving for R gives us a radius of approximately meters, which is about 140 trillion light years, or 10,000 times bigger than the size of the observable universe. So maybe space itself wouldn't even be big enough to handle such a massive sand ball.

Carrying the sand idea a little further, imagine there was a huge interstellar alien for whom the Earth appeared to be as small as a grain of sand is to us. Now, suppose this being lived on a giant planet, the planet Gigantica, as big, relative to the alien, as the Earth is to us. 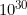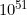This would imply that the volume of Gigantica was in proportion to the Earth as the Earth is to a grain of sand, about times as big; so Gigantica itself would be about cubic meters in volume. 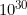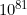If, in turn, there were a still larger alien for whom Gigantica looked like a grain of sand and who lived on an even larger planet, the planet Humonga, say, then Humonga would have to be times as big as Gigantica, for a volume of cubic meters. 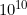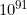Now, if yet an even larger alien, from the planet Ginormica, looked down on Humonga as a tiny grain of sand, it would require Humonga-balls to comprise a volume of cubic meters, which you'll recall was the volume of space taken up by a googol grains of our puny Earth-sand. 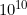Back here on Earth, grains of sand is 10 cubic meters, about the volume of a nice 10 meter by 10 meter patch of beach (assuming a depth of 10 centimeters). So on Ginormica, this giant giant giant alien could kick back in a beach chair, sip a giant giant giant beer and build a giant giant giant sand castle out of those googol grains with plenty of sand left over to get in its megashoes.

-DrM