Boys and/or Girls

Here's a classic probability puzzler that's been floating around in the aether recently. The particular question came from my good friend Short Round over at www.alt85.com:

Dear Doctor Math,
You know that a certain family has two children, and that at least one is a girl. But you can't recall whether both are girls. What is the probability that the family has two girls? I stole this question from the infernet.
SR

First let me give the answer, and then I'll talk about why it sounds wrong.

The answer is . Let's call the two kids Ashley and Whitney (could be boys' or girls' names, get it?); there are initially four possibilities for the genders of (Ashley, Whitney) without the extra restriction that one has to be a girl. They are: (boy, boy), (boy, girl), (girl, boy), (girl, girl). Assuming that each kid is a boy or a girl with equal probability and that the genders of the kids are independent from each other, each pairing has probability because we have no information to prefer one over the others. Now, with the added information that at least one is girl (we saw some moisturizer in the bathroom but we don't know whose it is), we can eliminate the (boy, boy) possibility. However, we still have no information to indicate that any one of the remaining three pairings is more likely than any other, and so the probability of each of them is , given the new information. Thus, the chance of there being two girls is .

Now, as I mentioned before, this is a classic brainteaser, which really just demonstrates the weird counterintuitive things that can happen when you ask for the probability of an event given some unusual information. Most people balk at the idea of there being a chance of a kid being a boy, because they're so conditioned to think of the odds always being equal, but since probability is an expression of the information you have about some event and the consequences of said information, it's entirely possible to construct bizarre examples like this one (it's hard to contrive a scenario where you would know just that one of the kids is a girl but not know which one). Strangely, if you know the oldest child is a girl, then the probability of the other being a girl goes back up to .

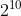
To show what would happen if you took this a few steps further--let's say you had a whole busload full of 10 people with androgynous names and you didn't know the genders of any of them. To help us tell them apart, let's refer to each by his/her seat number, 1 through 10. There are two possibilities for each person, and they're independent of each other, so to start off with, there are , or 1024, possible configurations for the gender line-up, all equally likely. Now, suppose you find Zac Efron posters in the duffel bags of nine out of the ten people, so you know there are at least nine girls but somehow you don't know who they are. Given that information, you can eliminate all but 11 remaining possibilities: either they're all girls, or there's one boy, and he's sitting in one of 10 possible seats. Again, we have no reason to think one of these outcomes is more likely than any other; thus, the resulting probability that you actually have a bus full of all girls is .

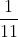
Like puberty, probability can be scary sometimes, but that's just life.

-DrM